Greetings, and welcome to another article of Magic Theory, which is a bit different than my Miracle-centric content that you may be accustomed to. I will neither tell you which deck to play at your next Legacy event, nor how you should be preparing for tournaments to come. First we will take a look at the principles of Game Theory. Then I will try to convey the messages that we learned by taking a look at these principles to our beloved game, Magic: the Gathering. So let’s get it going, right?
So how do we start? I guess it’s correct to talk about the term “Game Theory” first, right? It is basically a term that originated from mathematics, but don’t worry – I’ll give my best to leave mathematical analysis aside as good as I can. Fundamentally speaking, Game Theory is about the prediction of events that succumb to the rules of cooperation and conflict.
Game Theory can apply to many fields, ranging from mathematics to sociology, including many things in between. A statement like “life is a game” – isn’t as far off as one might think. Many, if not most, interactions can be boiled down to a structure, which could be described as a game.
Now let’s get into some examples where you can apply Game Theory before looking at the aspects that we, as Magic players can profit from, shall we?
One of the most well-known examples is the game of “even or odd” which I’ll cover in a bit. Other examples are rush-hour traffic, political manifestos and even courtship or the war that Adolf Hitler and Josef Stalin brought over the whole world. All of those interactions can be understood as a game, with a more or less terrible outcome.
Nash Equilibrium
In order to proceed with our journey into the realms of Game Theory we have to understand one of the main pillars of said domain. It’s the so called Nash Equilibrium, which was postulated by John Nash, whose life you might be familiar with due to the multiple Oscar winning film “A Beautiful Mind.”
Even though the above mentioned topic is a part of the purely mathematical part of Game Theory I will give my best to convey the message without any unnecessary mathematical operations. The first thing you have to know is that the Nash Equilibrium only works for non-cooperative games. So this obviously won’t work for games where the players can work together, which makes it a perfect premise for our beloved game of Magic. The next step we have to take is to look at what the Nash Equilibrium actually says, before delving into some examples.
Said theorem is applicable to a non-cooperative game where both players are supposed to know the equilibrium strategies of the other player, and no player would therefore gain anything by changing their own strategy.
I will illustrate this with the help of a couple of classic examples. All of the following examples will be done with the help of two fictitious test persons named Alice and Bob. In the above mentioned “even or odd” example we have two players. They will flip two coins. Alice wins if both coins land on the same side, so two “heads” or two “tails” coins, while Bob will prevail if the sides show different images.
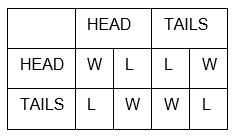
On the left column we have the results of Alice, and Bobs on the right. This chart displays the above mentioned distribution of their respective wins (W) and losses (L).
Another example that is quite different from the zero-sum game that “even or odd” was is the so called “coward’s game.” Imagine that Alice and Bob would each steer a car. Those cards move towards them on a narrow street, so it won’t be possible that both drive fast. Either one or both have to slow their speed down in order to be able to pass through this narrow street. So how would the chart look this time? Different from the last one, correct. But instead of “W” and “L” I’ll now use figures to indicate if and to which extent the goal is reached.
Once again we have Alice’ results in the left column, while Bob occupies the right one again. So let’s break this chart down, shall we? In the upper left we have the case that both of the drivers slow down in order to enable a safe passage. It works out as nobody is endangered – so this case is rewarded with the positive number of “3.”
On the bottom right box we have the exact opposite. Both drivers will not slow only slow down, they will even accelerate, leading to the expected disaster. They will most likely crash right into each other – displayed by the negative figures of “-1.”
The two remaining chart-chapters show the most important part of this very thought-experiment. In both examples one of the two drivers, Alice or Bob, will slow down, while the other one will accelerate. So that’s interesting. What we see here is that the one slowing down will not receive a negative figure, due to not crashing, despite being slowed down considerably. The rushing one, on the other hand, gets rewarded with an outstanding figure of “4,” which is higher than anything else.
So what can we take from this? The best strategy seems to be driving fast, if the other one is slowing down, right? Well, as you can imagine it won’t be that easy – as you cannot simply predict the actions and decisions of your counterpart most of the time.
The Nash Equilibrium to the second example is “fast” + “slow” as well as “slow” + “fast.” But what does this mean? It simply indicates that the best choice is either one of these examples, as it will result in a “4” for one of the participants. But the whole story gets even more interesting when you add another layer to the equilibrium. Let’s assume that there is a very well-known rule that describes how you should behave in this situation. This very rule tells you to slow down. So now both drivers know, that the respectively other driver knows this rule and will therefore slow down. But if Alice knows, that Bob knows that he should slow down, it’s pretty obvious that she will accelerate. But what if Bob knows that she will accelerate, and what if Alice knows that Bob knows that Alice knows that Bob knows…
This ends in an “infinite regress” which is a regress into an infinite sequence of propositions in an attempt to find the truth of the proposition Px on the truth of the proposition Px+1 and so on. But I wouldn’t bring up this example if there wasn’t at least a possibility to escape this circle, right? Well, there is a solution, despite not being as satisfying as I’d like it to be. In order to come to a conclusion you have to assume that the plans of your opponent are self-consistent. This is the only way to break this infinite regress without destroying the concept of an equilibrium, which is what I’ll come to, now.
So after all this examples and explanations it’s finally time to talk about what the Nash Equilibrium actually is before delving into the Magic aspect of all of this, and what we can learn from it. The basic theorem behind the Nash Equilibrium can be described as:
“If there is a set of strategies with the property that no player can benefit by changing her strategy while the other players keep their strategies unchanged, then that set of strategies and the corresponding payoffs constitute the Nash Equilibrium.“
So let’s get back to the example one last time, shall we? If both players drive slowly, then one player could easily switch their strategy on their own, with the benefit of basically “+1” from “3” to “4.” So this is clearly no Nash Equilibrium. But look at the chart I was talking about earlier. Two quarters of said chart are in bold face, which should indicate something. Those two scenarios do represent a perfect example of a Nash Equilibrium. Let’s think it through for once, shall we?
So what if Alice decides to slow down, while Bob decides to go faster? What happens if Alice on her own changes her strategy? Both are rushing, so it’ll end in a disaster, with “-1” point for both, which will result in a direct loss one point for Alice and five for Bob. Obviously not the best outcome. And what if Bob wants to change his strategy of driving fast while Alice drives slowly? Alice would go from “0” to “3” while Bob would lose one point, falling down to “3” as well, making this scenario not favorable for Bob to choose. So we have a set of strategies, and there is no way either of them wants to change their strategy on their own. That’s what the Nash Equilibrium is all about.
A Magic Look at Things
Enough of dry theory for once. Let’s see if we can apply what we learned to Magic, in order to profit from it in one way or another, right?
The first thing that comes to my mind that might be explainable with the Nash Equilibrium is the Legacy metagame all by itself. In Legacy there is a large variety of established, well known, and doubtlessly powerful decks. You have Delver of Secrets-based tempo decks, Deathrite Shaman-based midrange ones, as well as Stoneforge Mystic and Counterbalance-centric control decks alongside a plethora of combo. Nothing out of the ordinary, we’ve been used to it.
But once in a while you see decks like 12-Post or Goblins pop up, and be more or less successful. What is the reason you see decks like this, and is it a good idea to play them? Well, those decks are mostly being piloted by players who’ve been playing them for a while and are kind of masters of their very specific archetype or deck. This makes them win more often than they probably should. So is this a good idea to pick up a deck like this when you’ve been playing a tier-one deck like RUG Delver or Shardless BUG for the time being? Remember what we learned about what a Nash Equilibrium was about, assuming that the Legacy metagame does indeed come close to said state. If this was the case then changing from a tier-one deck to one of the rogue-based decks is not worthwhile, as long as your opposing counterpart, in this case – the metagame as a whole, does not change their deck choice as well.
You obviously have to take several other factors into consideration, just as the player itself with his or her very specific variations of format familiarity, skill, and all of the other big or small factors that influence the outcome of a game of Magic. Oh, and there is luck as well.
But when approaching this topic from the macro level you quickly see that the Legacy metagame really is on kind of a Nash Equilibrium, as the best choice is playing one of the well-known decks. I am well aware that this can be misunderstood quickly. I am not saying that playing the best decks is the best way of winning. At least not the way one might think it means. There are many decks that would be good. But they are not right now, not in the current metagame. Take 12-Post as an example. It’s really hard to not win against Miracles, and DeathBlade is pretty easy to overcome too. But as long as the format consists of Wasteland + Combo decks to some extent this deck simply isn’t that great of a choice. Even though it’s good by itself in a vacuum. Thought processes like this might be familiar to you from metagame considerations. And this is exactly what I want to aim for. Metagame considerations are considerations based on the above mentioned equilibrium. Neither of the players has the intention to change their strategy as long as others do not do so, too.
What you can take away from this is pretty simple. If you want to compete at a high level in Legacy, don’t just take a deck you like. Take a deck you like, chosen from a plurality of decks that equal decisions which happen to be in a Nash Equilibrium. But choosing a right deck is something way more complex – and I plan on focusing on this topic in one of the following articles.
Bluffing in Magic
The next topic I want to touch on is a topic that might not be part of your everyday game of Magic. I am talking about bluffing. Even though bluffing can certainly be done at your kitchen table it is a certain part of high stake tournaments just as a Day 2 of a Grand Prix, a SCG Invitational, or a Pro Tour. It’s very hard to be successful at these kind of tournaments without knowing what bluffing is about, in our game. You don’t have to be a master of bluffing, but knowing about this is essential to your overall success.
But I won’t be telling you how to bluff correctly, as this will probably be part of another future article of mine. What I’ll be taking a look at is a problem in bluffing that comes very close to a problem that we’ve had in our observations of the Nash Equilibrium earlier. Have you heard of the “wine in front of me” – game/principle? No? It’s a game of life and death, basically. It boils down to you sitting down with your archenemy, and while you are looking away he is poisoning one of the two goblets standing at the table. One at your side, one at his. Now it’s your turn to choose whether you would like to swap the goblets or not, before you both drink at the same time. One of you will die, the winner will take the prize.
So what are the possibilities? Your opponent could just have put the poison in his goblet, because he thought, that you were dumb enough to think, that he would have put it into your goblet and would therefore switch the goblets. But what if he knew that you were aware of this line of thought and would therefore poison your goblet? But if you knew, that he knew, that you knew, that he knew…
You see where this is going, regression ad infinitum once again. You could just keep going, but all that would keep changing is just one move. If you think that your opponent is bad you would change the goblets, if you think the he knew what your thought process would be then you wouldn’t change, and if you think that he knew that you knew you would change it again. You get the point.
But you have to stop at some point, in order to transfer this to real tournament play. Moreover this very action comes down to your assessment and evaluation of your opponent. Just as we did earlier when examining the Nash Equilibrium you have to think of your opponent as a stable and consistent playing human being. You can’t just lose yourself in infinite thoughts about what he might have thought that you thought and so on. At one point of the game you have to make a concrete determination of how good your opponent might be. Is he really just keeping the mana for Dissipate, or does he want me to think that he has Dissipate, or does he want me to think that I think that he has no Dissipate? – I’d suggest stopping at this point – every consideration above this one seems just like wasted energy to me.
The last point I want to talk about is assessing roles. Despite being unable to draw indisputable links to the Nash Equilibrium I still believe to have found similarities that can be of use. Let’s take the most thrilling match in nowadays Legacy format as an example. The Miracles mirror match. While pre-boarded matches are highly dependent on how many white cards you are forced to work with, the sideboarded ones are amongst the most interesting games in Magic, at least for me.
If everything goes according to plan both players in an UWr vs. UWr mirror match will do nothing. Literally. All they want to deploy in the early game is measurements of card quality like Sensei’s Divining Top or Ponder. Some hands force either player into a Turn 2 Counterbalance, but most of the time the plan is to do nothing. You have your Top, and your next goal is to make each land drop while filling your hand with as many powerful cards as possible. This strategy counts for both of the players. Neither sees a reason to change his reason, without the other one doing so, too – for the most part. Doesn’t this sound familiar? It sure does!
Both players will try to keep drawing as much gas as they can for as long as possible, or until the first one act, which is either motivated by this player being less informed about the optimal plan, which is a premise for most game theory examples, or due to strategic reasons that allow him to break the build-up of cards, Vendilion Clique is the prime example. Most experienced Miracle players will be well aware of this, equally to the fact that you do not always have the means to follow said guideline.
Something similar appears to be the case when you are in a Delver of Secrets mirror. While one side is beating down the other one – many cards on both sides change in value explicitly. The player who is beating down has no intention to change his strategy and go on defense all of a sudden. Moreover, the player who is being beaten down will not change his strategy either for the time being – as it’s tough to start a race when your opponent has been working on your life total already. Cards like Stifle and Hymn to Tourach, in order to stay in the Delver-territory, change drastically dependent on the role they are used, especially in a 75-card mirror. This doesn’t only affect the way you play your action cards – but also the way you play your cantrips like Ponder or Brainstorm.
So what can you take away from today’s article? When you are observing a decision-necessitative incident both in and outside your game of Magic – think about the possibility of it being at Nash Equilibrium and what this means to your choice. Whether you should be choosing at all or not. I think thought processes like this will help you improve in your matches of Magic, as well as many other problems that might arise in your life. Remember, life is nothing but a game. A huge, complex, intriguing and fascinating game, but nothing but a game.
Did you like this article? What didn’t you like? Where should I be improving? What would you like to see next? Let me know in the comment section below.
Greetings,
Philipp
Sources:
Roger McCain: Game Theory: A Nontechnical Introduction to the Analysis of Strategy
Ken Binmore: Spieltheorie